2016年07月18日
できるだけわかりやすく説明してみるという実験:遺伝的プログラミング
遺伝的アルゴリズムは個体の性質を表すパラメーターを「遺伝子」と見立て、それを交配することによってより優性な個体を生成し、それを繰り返すことによって最適なパラメーターの組み合わせになるように「進化」させるものであった。
このときの遺伝子は、その個体が持つすべてのパラメーターを一本に並べ、その任意の点で交差させることで新しい個体の遺伝子を作る、というものであった。
つまり、各個体が持つパラメータの構成は固定であり、構成自体が変わるものではない。
このときの遺伝子は、その個体が持つすべてのパラメーターを一本に並べ、その任意の点で交差させることで新しい個体の遺伝子を作る、というものであった。
つまり、各個体が持つパラメータの構成は固定であり、構成自体が変わるものではない。
これに対し「遺伝的プログラミング」というものは全く違う発想のものである。
遺伝的"プログラミング"という名前にもあるとおり、遺伝的プログラミングでは、「プログラムを進化させることによって優性の個体を作り出そう」という考え方である。
ここでの「プログラム」とは、「関数」と考えて良い。
以前、「できるだけわかりやすく説明してみるという実験:関数、メソッド」で説明したように、プログラミングにおける関数とは、「ある値を受け取り、ある処理を行って、その結果を戻り値として返すもの」のことである。
たとえば「aという値を与えればaを半径とする円の面積を返す」というようなもののことである。
遺伝的プログラミングでは、遺伝的アルゴリズムのようにその遺伝子を一本の線上に並べて扱うのではなく、ツリー構造で表す。
ここでの「ツリー構造」とは、「ノード」と呼ばれる節点と、そのノードを繋ぐ「エッジ」と呼ばれる枝で構成された木の構造をしたものである。
たとえば下図では"2"、"+"、"a"と書かれた円がノードで、それらを繋ぐ枝がエッジである。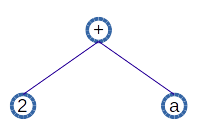
遺伝的"プログラミング"という名前にもあるとおり、遺伝的プログラミングでは、「プログラムを進化させることによって優性の個体を作り出そう」という考え方である。
ここでの「プログラム」とは、「関数」と考えて良い。
以前、「できるだけわかりやすく説明してみるという実験:関数、メソッド」で説明したように、プログラミングにおける関数とは、「ある値を受け取り、ある処理を行って、その結果を戻り値として返すもの」のことである。
たとえば「aという値を与えればaを半径とする円の面積を返す」というようなもののことである。
遺伝的プログラミングでは、遺伝的アルゴリズムのようにその遺伝子を一本の線上に並べて扱うのではなく、ツリー構造で表す。
ここでの「ツリー構造」とは、「ノード」と呼ばれる節点と、そのノードを繋ぐ「エッジ」と呼ばれる枝で構成された木の構造をしたものである。
たとえば下図では"2"、"+"、"a"と書かれた円がノードで、それらを繋ぐ枝がエッジである。

遺伝的プログラミングでは、上図を"2+a"という関数であると考える。
"+"の子供が"2"と"a"であり、その子供を"+"する、ということである。
そしてこのツリー構造がそのまま遺伝子として考えられる。
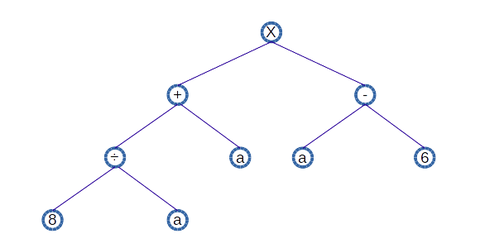
この遺伝的プログラミングにおける「ツリー構造での関数の表現」のもう少し複雑な例を挙げてみると、、、
これは、"( (8÷a) + a ) x (a - 6)"という関数である。
常に一番深いノード(この図では左下の"8"と"a")から計算をして、一番上のノード(この図では"X")の計算を最後にする、ということになる。
遺伝的プログラミングにおける交配は、遺伝的アルゴリズムのように遺伝子の長さ、形が同じである必要はない。
上図は先程の"( (8÷a) + a ) x (a - 6)"と、新たに"(a+2) ÷ 4sin(a)"というものを右側に並べたものである。
見て分かる通り、これらはツリー構造の形自体が違うし、ノードの数も異なる。
遺伝的プログラミングでは、このような場合であっても交配が可能である。
遺伝的プログラミングの交配は、二つの個体を表すツリー構造の任意のノードをそれぞれひとつずつ選び、それ以下の部分を入れ替える、ということを行う。
これにより次の世代として、両親の特徴を引き継いだ新たな個体が生まれる、というわけである。
上図の例では、"( (8÷a) + a ) x (a - 6)"と"(a+2) ÷ 4sin(a)"という両親から、"4sin(a) x (a - 6)"という個体と、"(a + 2) ÷ ( (8 ÷ a) + a )"という新たな個体が生まれたことになる。
こらは両親のいずれとも異なる新しい関数を持った個体であるが、両親の特徴を引き継ぐものであると言える。
このようにしてできた新しい世代のうちから、より優性な個体を選択し、優性なものどうしをかけあわせる、ということを繰り返すうちに、優性な種として進化していき、優性な結果を出す関数が得られる、というわけである。
ここで「関数」と呼んでいるものは、「値を与えたら計算した値を返す」というものにとどまらず、そこには処理が伴う、という側面もあることを思い出そう。
たとえばそれが「ロボットを動かす」という関数であった場合、この遺伝的プログラミングで関数を進化させていくことで、目的を満たす動きをするロボットに進化していく、ということが可能になる。
そして、その遺伝子がツリー構造で書かれ、その構造が変わっていくということも可能であるため、予想を遥かに超えた新しいものが生まれてくる、ということが期待できるものである。
"+"の子供が"2"と"a"であり、その子供を"+"する、ということである。
そしてこのツリー構造がそのまま遺伝子として考えられる。
この遺伝的プログラミングにおける「ツリー構造での関数の表現」のもう少し複雑な例を挙げてみると、、、
これは、"( (8÷a) + a ) x (a - 6)"という関数である。
常に一番深いノード(この図では左下の"8"と"a")から計算をして、一番上のノード(この図では"X")の計算を最後にする、ということになる。
遺伝的プログラミングにおける交配は、遺伝的アルゴリズムのように遺伝子の長さ、形が同じである必要はない。
上図は先程の"( (8÷a) + a ) x (a - 6)"と、新たに"(a+2) ÷ 4sin(a)"というものを右側に並べたものである。
見て分かる通り、これらはツリー構造の形自体が違うし、ノードの数も異なる。
遺伝的プログラミングでは、このような場合であっても交配が可能である。
遺伝的プログラミングの交配は、二つの個体を表すツリー構造の任意のノードをそれぞれひとつずつ選び、それ以下の部分を入れ替える、ということを行う。
これにより次の世代として、両親の特徴を引き継いだ新たな個体が生まれる、というわけである。
上図の例では、"( (8÷a) + a ) x (a - 6)"と"(a+2) ÷ 4sin(a)"という両親から、"4sin(a) x (a - 6)"という個体と、"(a + 2) ÷ ( (8 ÷ a) + a )"という新たな個体が生まれたことになる。
こらは両親のいずれとも異なる新しい関数を持った個体であるが、両親の特徴を引き継ぐものであると言える。
このようにしてできた新しい世代のうちから、より優性な個体を選択し、優性なものどうしをかけあわせる、ということを繰り返すうちに、優性な種として進化していき、優性な結果を出す関数が得られる、というわけである。
ここで「関数」と呼んでいるものは、「値を与えたら計算した値を返す」というものにとどまらず、そこには処理が伴う、という側面もあることを思い出そう。
たとえばそれが「ロボットを動かす」という関数であった場合、この遺伝的プログラミングで関数を進化させていくことで、目的を満たす動きをするロボットに進化していく、ということが可能になる。
そして、その遺伝子がツリー構造で書かれ、その構造が変わっていくということも可能であるため、予想を遥かに超えた新しいものが生まれてくる、ということが期待できるものである。