2016年06月01日
フラクタル:形而上のなめらかな面
ベノワ・マンデルブロが体系化したフラクタル幾何学は大きく次の3点について語っている。
非整数次元、自己相似、微分不可能性。
ここで、フラクタル幾何学についてご存じない方のために、その説明に最も使われるコッホ曲線
について。
コッホ曲線は、上記の3点を説明するのに最も分かりやすい例だろう。
以下、Wikipediaよりコッホ曲線の描き方の図を拝借。
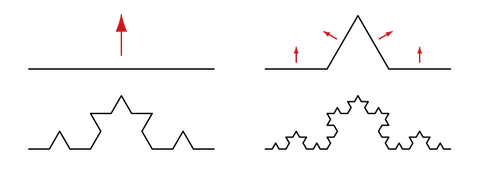
まず、一本の直線を4等分し、真ん中の2本を山形に折る。これが基本形。(右上)
4本の部分線を同じく4等分し、同じようにそれぞれを山形に折る。(左下)
これを繰り返す。(右下)
この繰り返しを無限に繰り返すことにより、コッホ曲線ができあがる。
この繰り返しを行うことによって、無機的だった基本形(右上)がどんどん有機的な
形に見えてくるようになる。
本来、線は一次元のものであることは明白であるが、その線で構成されているはずの
コッホ曲線は、どんどん面に近づいていく。
これをもう少しわかりやすく表しているのがヒルベルト曲線である。
これは基本形をカタカナのコの字形にしたものだ。同じくWikipediaより。

ヒルベルト曲線では、上記の「線が面に近づいていく」というのが分かりやすい。
そしてマンデルブロはこれを一次元と二次元の中間にある、1.X次元と定義し、
それまで整数でしか表されることのなかった次元の表現に少数を持ち込んだ。
マンデルブロの定義は感覚的なものにとどまらず、そのフラクタル図像が非整数次元で
何次元になるのかという計算式も定義している。
コッホ曲線とヒルベルト曲線を見ると「自己相似」の意味もよく分かる。
その形を構成するどの部分を見ても、その全体像の縮小相似形になっている。
これを自己相似形といい、これは現実世界のあらゆるところに見られるものであるという。
ところで、これらの直線で構成されたフラクタル図形を「曲線」と呼ぶことに違和感を感じない
だろうか?
フラクタル幾何学で「微分不可能性」というときのポイントがここにある。
ふたたびコッホ曲線に戻って考えよう。
コッホ曲線を無限に描き続けたことを考えた場合、その中のどの部分をとっても、尖った部分
が現れることになる。つまり、無限に描き続けられたコッホ曲線はどの部分をとっても
微分不可能である、ということである。
これについても、現実世界のすべてのものに当てはまることである。
この世に存在するあらゆるものは、その最小部分まで拡大して観察すると、かならず尖った部分
が現れることになる。たとえどれだけなめらかな面を持った物質であっても、それは分子で
構成されていて、つまり分子レベルではなめらかではなくなる。
「コッホ曲線」「ヒルベルト曲線」というときの「曲線」とは、この本来なめらかなはずの曲線
というものが形而上のもので、実はあらゆる曲線が微分不可能である、ということを浮き彫りに
するものである。
浮き彫りにされたものを、単にアイロニーとしてだけ捉え、「ああ、確かにこの世には曲線も
曲面も存在しないなあ」という理解で終わるのはもったない。
確かにこの世には曲線も曲面も存在しない。直線も平面もすべて形而上のもの。
ここで気づくべきことは、実際には存在しないはずの曲線、曲面、直線、平面たちをそうであると
認識する人間の力である。形而上のものを抽象的に捉える能力。日本的な言い方をすれば
「見立て」。
フラクタル幾何学は、近代科学の中で無意識のままものごとを抽象的に捉え、その事自体を
忘れていたことを思い出させ、さらには人間に形而上のものを抽象的に捉える能力が備わって
いることを思い出させるものであった。
非整数次元、自己相似、微分不可能性。
ここで、フラクタル幾何学についてご存じない方のために、その説明に最も使われるコッホ曲線
について。
コッホ曲線は、上記の3点を説明するのに最も分かりやすい例だろう。
以下、Wikipediaよりコッホ曲線の描き方の図を拝借。

まず、一本の直線を4等分し、真ん中の2本を山形に折る。これが基本形。(右上)
4本の部分線を同じく4等分し、同じようにそれぞれを山形に折る。(左下)
これを繰り返す。(右下)
この繰り返しを無限に繰り返すことにより、コッホ曲線ができあがる。
この繰り返しを行うことによって、無機的だった基本形(右上)がどんどん有機的な
形に見えてくるようになる。
本来、線は一次元のものであることは明白であるが、その線で構成されているはずの
コッホ曲線は、どんどん面に近づいていく。
これをもう少しわかりやすく表しているのがヒルベルト曲線である。
これは基本形をカタカナのコの字形にしたものだ。同じくWikipediaより。

ヒルベルト曲線では、上記の「線が面に近づいていく」というのが分かりやすい。
そしてマンデルブロはこれを一次元と二次元の中間にある、1.X次元と定義し、
それまで整数でしか表されることのなかった次元の表現に少数を持ち込んだ。
マンデルブロの定義は感覚的なものにとどまらず、そのフラクタル図像が非整数次元で
何次元になるのかという計算式も定義している。
コッホ曲線とヒルベルト曲線を見ると「自己相似」の意味もよく分かる。
その形を構成するどの部分を見ても、その全体像の縮小相似形になっている。
これを自己相似形といい、これは現実世界のあらゆるところに見られるものであるという。
ところで、これらの直線で構成されたフラクタル図形を「曲線」と呼ぶことに違和感を感じない
だろうか?
フラクタル幾何学で「微分不可能性」というときのポイントがここにある。
ふたたびコッホ曲線に戻って考えよう。
コッホ曲線を無限に描き続けたことを考えた場合、その中のどの部分をとっても、尖った部分
が現れることになる。つまり、無限に描き続けられたコッホ曲線はどの部分をとっても
微分不可能である、ということである。
これについても、現実世界のすべてのものに当てはまることである。
この世に存在するあらゆるものは、その最小部分まで拡大して観察すると、かならず尖った部分
が現れることになる。たとえどれだけなめらかな面を持った物質であっても、それは分子で
構成されていて、つまり分子レベルではなめらかではなくなる。
「コッホ曲線」「ヒルベルト曲線」というときの「曲線」とは、この本来なめらかなはずの曲線
というものが形而上のもので、実はあらゆる曲線が微分不可能である、ということを浮き彫りに
するものである。
浮き彫りにされたものを、単にアイロニーとしてだけ捉え、「ああ、確かにこの世には曲線も
曲面も存在しないなあ」という理解で終わるのはもったない。
確かにこの世には曲線も曲面も存在しない。直線も平面もすべて形而上のもの。
ここで気づくべきことは、実際には存在しないはずの曲線、曲面、直線、平面たちをそうであると
認識する人間の力である。形而上のものを抽象的に捉える能力。日本的な言い方をすれば
「見立て」。
フラクタル幾何学は、近代科学の中で無意識のままものごとを抽象的に捉え、その事自体を
忘れていたことを思い出させ、さらには人間に形而上のものを抽象的に捉える能力が備わって
いることを思い出させるものであった。